- the dependence of the kinetic energy of the proton ejectile T_1 on its return distance to the axis z, on the kinetic energy of incoming beam particles T, and on the emission angle of the proton in the CM frame theta_CM.
- the dependence of cos(theta_CM), the cosine of the emission angle of the proton in the CM frame, on the kinetic energy of the proton ejectile T_1 and on its return distance to the axis z.
- the dependence of the nucleus excitation energy E_x on the kinetic energy of the proton ejectile T_1 and on its return distance to the axis z.
From equation (98) from HELIOS\_\_study\_of\_nuclear\_reactions\_in\_inverse\_kinematics.pdf, using (2.5), (2.6) and (2.7c) from Anna's licentiate, we get
\begin{align*}
\text{e}&=\frac{M_c^2 + m_1^2 - m_2^2}{\gamma \cdot 2{E_t}^2} - m_1 + \alpha \beta z= \ &=\frac{((m_a + m_b + T)^2 - (T+m_a)^2+m_a^2) + m_1^2 - m_2^2}{\frac{1}{\sqrt{1 - \frac{(T + m_a)^2 - m_a^2}{m_a + m_b + T}}} \cdot 2((m_a + m_b + T)^2 - (T+m_a)^2+m_a^2)} - m_1 + \alpha \left(\frac{\sqrt{(T + m_a)^2 - m_a^2}}{m_a + m_b + T}\right) z = \ &=\text{e(T,z)}.
\end{align*}
From equation (108) from HELIOS\_\_study\_of\_nuclear\_reactions\_in\_inverse\_kinematics.pdf, using (2.5), (2.6) and (2.7c) from Anna's licentiate for a constant $T$, we get
\begin{align*}
\text{e}&=-m_1 + \frac{-\sin^2(\theta) \alpha \beta \gamma^2 z + \cos(\theta) \sqrt{\alpha^2 z^2 + m_1^2 \left(1 - \sin^2(\theta) \gamma^2\right)}}{1 - \sin^2(\theta) \gamma^2}\ &=-m_1 + \frac{-\sin^2(\theta) \alpha \frac{\frac{\sqrt{(T_{\text{const}} + m_a)^2 - m_a^2}}{m_a + m_b + T_{\text{const}}} }{1 - \frac{(T_{\text{const}} + m_a)^2 - m_a^2}{(m_a + m_b + T_{\text{const}})^2}} z + \cos(\theta) \sqrt{\alpha^2 z^2 + m_1^2 \left(1 - \sin^2(\theta) \frac{1}{1 - \frac{(T_{\text{const}} + m_a)^2 - m_a^2}{(m_a + m_b + T_{\text{const}})^2}}\right)}}{1 - \sin^2(\theta) \frac{1}{1 - \frac{(T_{\text{const}} + m_a)^2 - m_a^2}{(m_a + m_b + T_{\text{const}})^2}}}\ &=\text{e($\theta$,z)}.
\end{align*}
From equation (1.21) from short\_kinematics.pdf combined with (98) and (108) from HELIOS\_\_study\_of\_nuclear\_reactions\_in\_inverse\_kinematics.pdf as well as (2.5), (2.6) and (2.7c) from Anna's licentiate, we get
\begin{align*}
\text{$E_x$}&=-m_2 + \sqrt{M_c^2 + m_1^2 - 2\gamma M_c (E - \alpha \beta z)}\ &=-m_2 + \sqrt{((m_a + m_b + T)^2 - (T+m_a)^2+m_a^2) + m_1^2 - 2\gamma \sqrt{(m_a + m_b + T)^2 - (T+m_a)^2+m_a^2} (E - \alpha \left(\frac{\sqrt{(T + m_a)^2 - m_a^2}}{m_a + m_b + T}\right) z)}\ &=\text{$E_x$(E,z)}.
\end{align*}
From equation (1.23) from short\_kinematics.pdf combined with (98) and (108) from HELIOS\_\_study\_of\_nuclear\_reactions\_in\_inverse\_kinematics.pdf as well as (2.5), (2.6) and (2.7c) from Anna's licentiate, we get
\begin{align*}
\cos(\theta_{CM})=\frac{\gamma(E\beta-\alpha z)}{\sqrt(\gamma^2(E-\alpha\beta z)^2-m_1^2)}=\text{$\cos(\theta_{CM})$(E,z)}
\end{align*}
From these equations, the expressions of these target variables can be evaluated on some parameter space and visualized as 2D Contour plots and heatmaps using EoM.py from gitlab/iss_sim:.png)
.png) Figure 1: Left: Right:
Figure 1: Left: Right:
.png)
.png) Figure 2: Left: Right:
Figure 2: Left: Right:
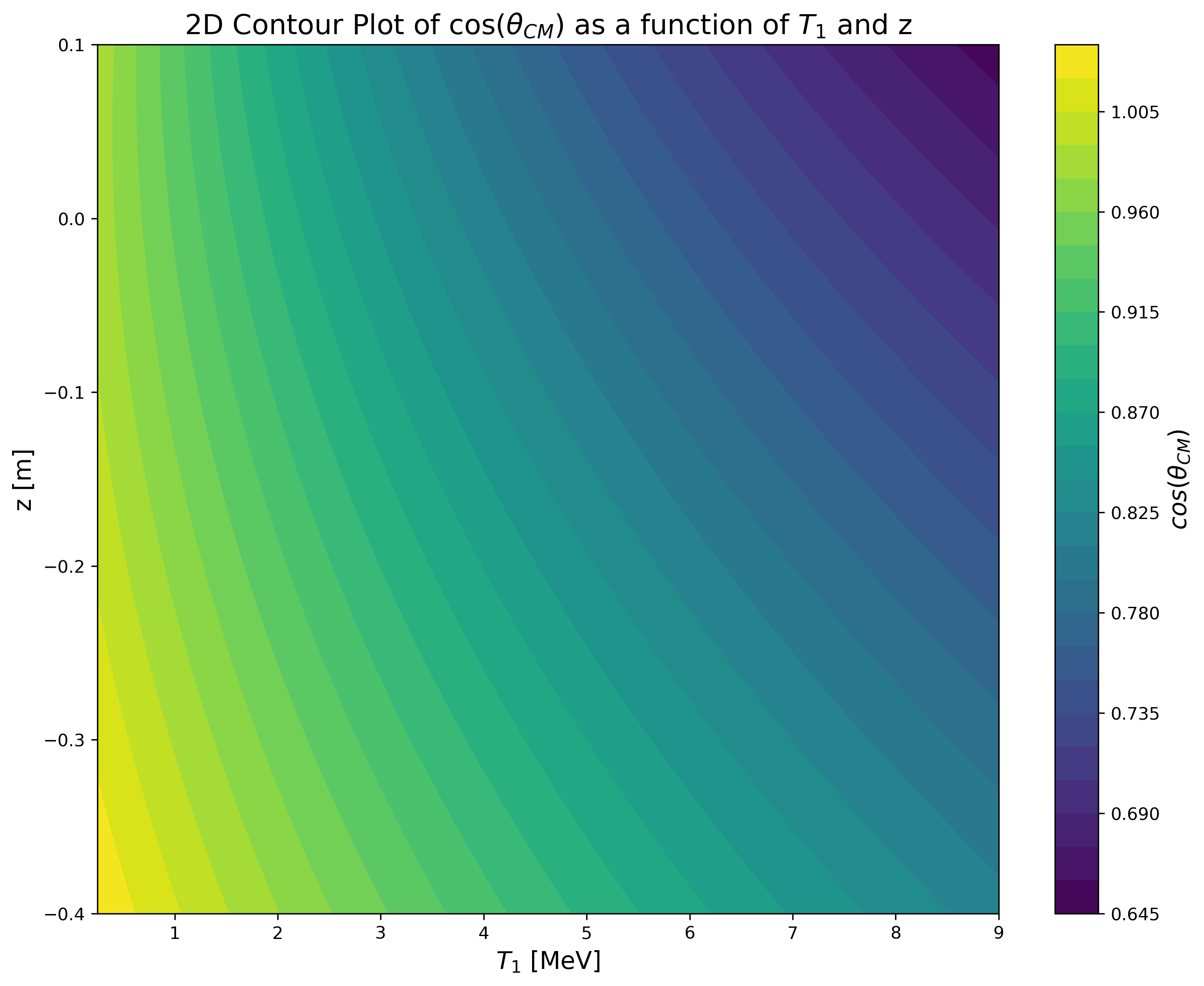
.png) Figure 3: Left: Right:
Figure 3: Left: Right:
.png)
.png) Figure 4: Left: Right:
Figure 4: Left: Right: Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Foswiki? Send feedback

