You are here: Foswiki>SubExp_Chalmers Web>ThetaExCorr (09 Jan 2024, AliceSvärdström)Edit Attach
-- AliceSvärdström - 08 Jan 2024
--test-13=dz=0.01cm,z0=-2.068cm,r=1.2cm,type=blackhole,enter,tree=1 \
--gun=d,dummy,T=0MeV,setboost,feed=target \
--gun=from=target,Ac229,dummy,T/u=8MeV/u,addboost,feed=cm \
-- gun=from=cm,p,Ac230:dummy:feed:setboost,Eexc=${Ex}MeV,isotropic,recoil,phasespace,feed=compound \
--gun-file=maxparticles=80,../ gunfiles / gun_230Ac_$ {Ex} MeV.txt,from=compound,boost \
--world=type=vacuum \
--fieldbox=d=200cm,Bz=2T \
--events=100000 \
--tree=helioscylinder${DIST}cm_${Ex}Mev.root The distance between array and target has been set to z0 = −2.068 cm, a 100000 events have been simulated for excitation energies Ex ∈ [6, 10] MeV for the nucleus. Figure 1 shows the distribution of θ in the lab frame of protonhits for different excitation energies Ex ∈ [6, 10] MeV. Figure 1: The distribution of θ in the lab frame of protonhits for different excitation energies Ex ∈ [6, 10].
In an initial attempt to convert θ from the lab frame to the center of mass frame, Catkin2.03 was used. The conversion between integer degrees 0-180 in the lab frame to the CM frame was calculated with the excel sheet for different excitation energies and the results are shown in Figure 3 below. The float values in the θ_lab distributions from Figure 1 was converted using Cubic Spline interpolation of the integer conversion from Catkin, resulting in the distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10] in Figure 3.
Figure 1: The distribution of θ in the lab frame of protonhits for different excitation energies Ex ∈ [6, 10].
In an initial attempt to convert θ from the lab frame to the center of mass frame, Catkin2.03 was used. The conversion between integer degrees 0-180 in the lab frame to the CM frame was calculated with the excel sheet for different excitation energies and the results are shown in Figure 3 below. The float values in the θ_lab distributions from Figure 1 was converted using Cubic Spline interpolation of the integer conversion from Catkin, resulting in the distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10] in Figure 3.
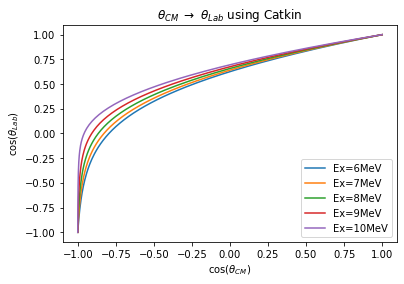 Figure 2: Conversion between the cosine value of integer degrees θ ∈ [0,180] in the lab frame to the CM frame calculated by Catkin2.03 for different excitation energies Ex ∈ [6, 10].
Figure 2: Conversion between the cosine value of integer degrees θ ∈ [0,180] in the lab frame to the CM frame calculated by Catkin2.03 for different excitation energies Ex ∈ [6, 10].
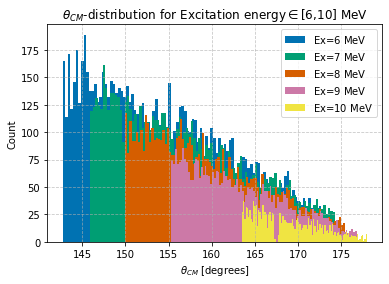 Figure 3: The distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10].
Figure 3: The distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10].
In ggland the Si-detector has been simulated as a mimic-cylinder (test-01) and a ”black hole''-screen (test-13) that excludes hits at the front and inside of the mimic-cylinder with the following bash-script:
--test-01=dz=37.465cm,z0=-20.8cm,ir=0.8cm,r=1.2cm,type=Si,enter,tree=1 \--test-13=dz=0.01cm,z0=-2.068cm,r=1.2cm,type=blackhole,enter,tree=1 \
--gun=d,dummy,T=0MeV,setboost,feed=target \
--gun=from=target,Ac229,dummy,T/u=8MeV/u,addboost,feed=cm \
-- gun=from=cm,p,Ac230:dummy:feed:setboost,Eexc=${Ex}MeV,isotropic,recoil,phasespace,feed=compound \
--gun-file=maxparticles=80,../ gunfiles / gun_230Ac_$ {Ex} MeV.txt,from=compound,boost \
--world=type=vacuum \
--fieldbox=d=200cm,Bz=2T \
--events=100000 \
--tree=helioscylinder${DIST}cm_${Ex}Mev.root The distance between array and target has been set to z0 = −2.068 cm, a 100000 events have been simulated for excitation energies Ex ∈ [6, 10] MeV for the nucleus. Figure 1 shows the distribution of θ in the lab frame of protonhits for different excitation energies Ex ∈ [6, 10] MeV.
 Figure 1: The distribution of θ in the lab frame of protonhits for different excitation energies Ex ∈ [6, 10].
In an initial attempt to convert θ from the lab frame to the center of mass frame, Catkin2.03 was used. The conversion between integer degrees 0-180 in the lab frame to the CM frame was calculated with the excel sheet for different excitation energies and the results are shown in Figure 3 below. The float values in the θ_lab distributions from Figure 1 was converted using Cubic Spline interpolation of the integer conversion from Catkin, resulting in the distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10] in Figure 3.
Figure 1: The distribution of θ in the lab frame of protonhits for different excitation energies Ex ∈ [6, 10].
In an initial attempt to convert θ from the lab frame to the center of mass frame, Catkin2.03 was used. The conversion between integer degrees 0-180 in the lab frame to the CM frame was calculated with the excel sheet for different excitation energies and the results are shown in Figure 3 below. The float values in the θ_lab distributions from Figure 1 was converted using Cubic Spline interpolation of the integer conversion from Catkin, resulting in the distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10] in Figure 3.
 Figure 2: Conversion between the cosine value of integer degrees θ ∈ [0,180] in the lab frame to the CM frame calculated by Catkin2.03 for different excitation energies Ex ∈ [6, 10].
Figure 2: Conversion between the cosine value of integer degrees θ ∈ [0,180] in the lab frame to the CM frame calculated by Catkin2.03 for different excitation energies Ex ∈ [6, 10].
 Figure 3: The distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10].
Figure 3: The distribution of θ in the CM frame of protonhits for different excitation energies Ex ∈ [6, 10].
Edit | Attach | Print version | History: r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r2 - 09 Jan 2024, AliceSvärdström
 Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Foswiki? Send feedback
